What is the Space of Spectral Sensitivity Functions for Digital Color
Cameras |
 | |
Camera spectral sensitivity functions relate scene radiance with captured RGB
triplets. They are important for many computer vision tasks that use color
information, such as multispectral imaging, color rendering, and color constancy.
In this paper, we aim to explore the space of spectral sensitivity
functions for digital color cameras. After collecting a database of 28
cameras covering a variety of types, we find this space convex and
two-dimensional. Based on this statistical model, we propose two methods to
recover camera spectral sensitivities using regular reflective color targets
(e.g., color checker) from a single image with and without knowing the
illumination. We show the proposed model is more accurate and robust for
estimating camera spectral sensitivities than other basis functions. We also
show two applications for the recovery of camera spectral sensitivities —
simulation of color rendering for cameras and computational color
constancy. |
Publications
Jun Jiang, Dengyu Liu, Jinwei Gu and Sabine Susstrunk.
What is the Space of Spectral Sensitivity Functions for
Digital Color Cameras?. IEEE Workshop on the Applications of Computer Vision (WACV), 2013.
Jun Jiang, Dengyu Liu, Jinwei Gu and Sabine
Susstrunk.Supplementary
Document (with proof and other experimental details).
|
Images
 |
|
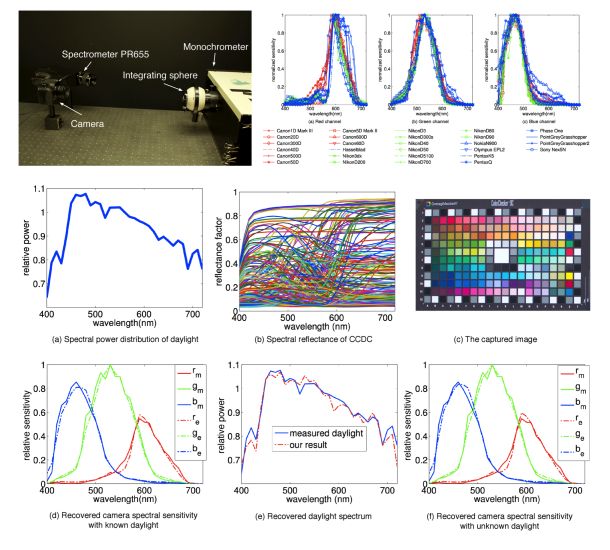
Experimental setup to obtain the groundtruth of spectral
sensitivity:
we have measured the spectral sensitivity functions for 28
cameras, including professional DSLRs, point-and-shoot, industrial and
mobile cameras (i.e., Nokia N900), using a monochromator and a spectrometer
PR655. At each wavelength, the camera spectral sensitivity in RGB channels
is calculated by c(λ) = d(λ)/(r(λ)t(λ)), where d(λ) is the raw data
recorded by the camera, r(λ) is the illuminant radiance measured by the
spectrometer, and t(λ) is the exposure time of the camera. All other settings
(i.e., ISO and aperture) remained the same during the measurement for each
camera. The procedure is repeated across the whole visible wavelength from
400 to 720nm with an interval of 10nm.
|
 |
|
The need of statistics prior of camera spectral sensitivities:
It is known that common color targets such as a colorchecker cannot
be used directly to recover camera spectral sensitivities under
conventional illumination (e.g., daylight, tungsten, fluorescent).
This is because the intrinsic dimensionality of real-world objects' reflectance is about 8, which is less than the number of unknowns in camera spectral sensitivities.
Direct inversion is not reliable, even with a small amount of
noise (1%).
|
 |
|
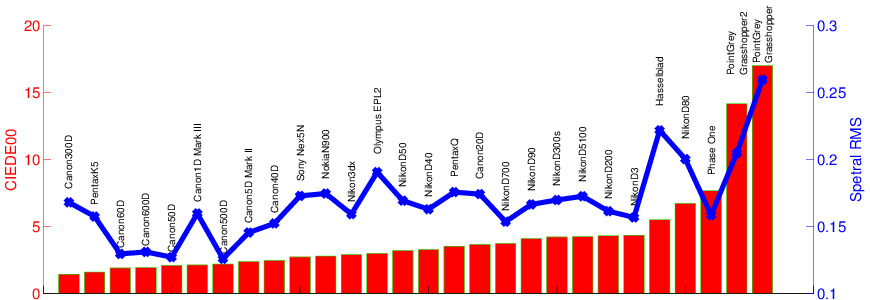
Luther condition evaluation:
A camera satisfies the Luther condition if
its spectral sensitivity function is a linear transformation of the
CIE-1931 2-degree color matching function. The Luther condition can be
evaluated by the RMS error between C2deg and TC, C2deg are the CIE-1931
2-degree color matching functions, and C are the measured camera spectral
sensitivities. Color difference (CIEDE00) is calculated between C2deg and TC
under CIE D65 illuminant and the 1269 Munsell color chips. Ideally,
spectral RMS and color differences are zero if a camera perfectly satisfies
the Luther condition. Overall, most cameras have a deviation from the
Luther condition, especially for the two industrial cameras.
|
 |
|
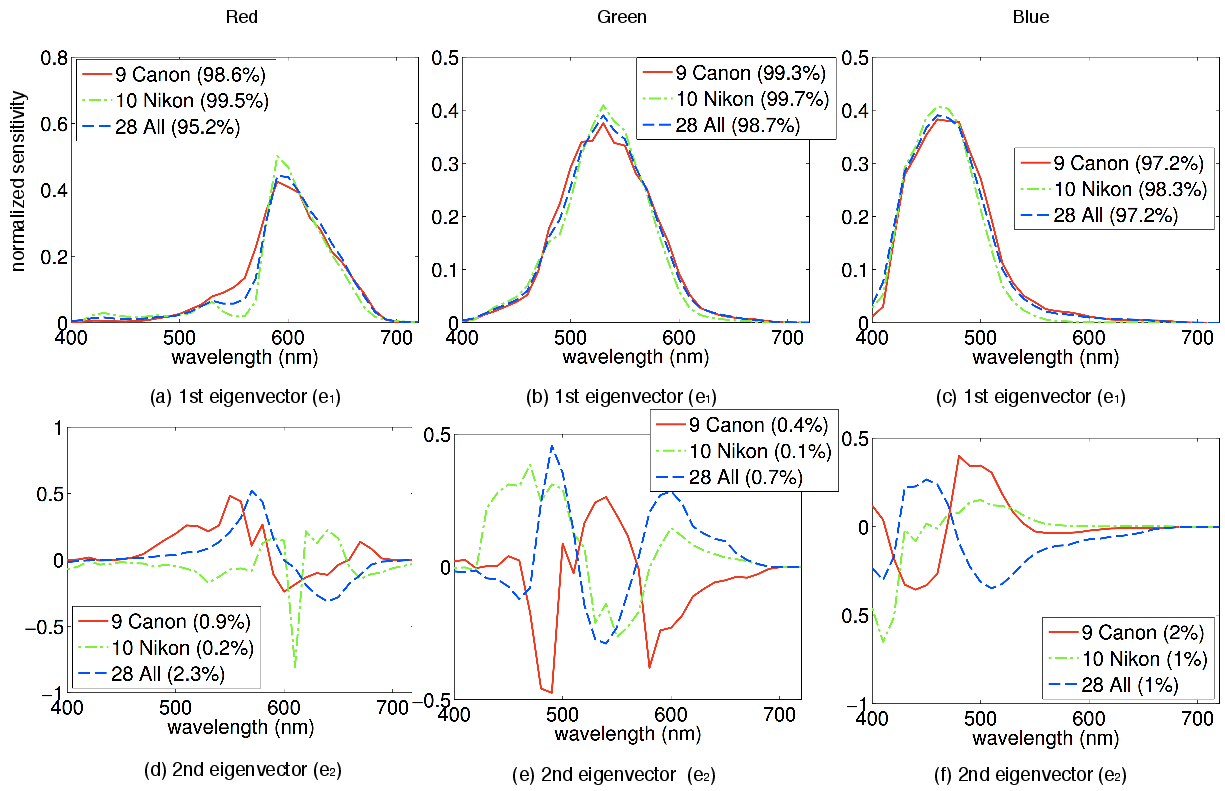
Principal components of camera spectral sensitivities:
The principal
components of camera spectral sensitivities. The three columns represent
the R/G/B channels, respectively. We performed PCA on Canon cameras, Nikon
cameras, and all 28 cameras. The 1st principal component accounts for over
95% of total variance for all three channels, and the first two principal
components accounts for over 97% of total variance. Thus, we model camera
spectral sensitivity functions as two-dimensional functions.
|
 |
|
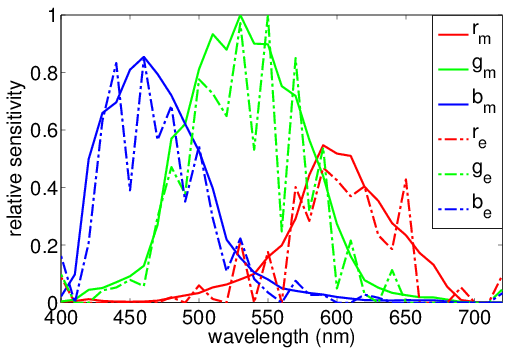
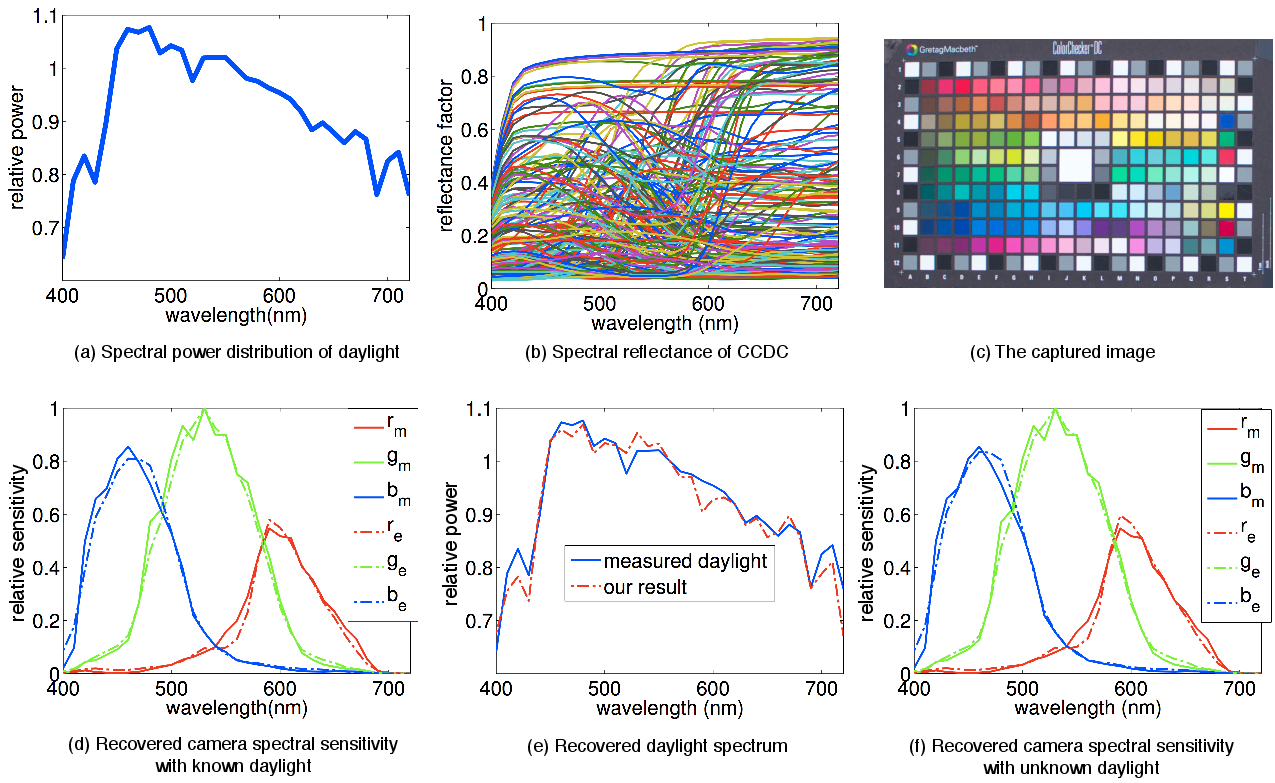
The recovery of camera spectral sensitivies of Canon 60D:
(a) The measured spectrum of a daylight. (b) The spectral reflectance of a
color checker DC. (c) The captured image (glossy and duplicate patches are
removed to avoid overweighting certain colors). (d) The recovered spectral
sensitivities with known daylight spectrum. By using a daylight model, we
can recover both the daylight spectrum (e) and the camera spectral
sensitivities (f). The subscripts m and e in (d) and (f) stand for the
measured and estimated camera spectral sensitivities, respectively.
|
 |
|
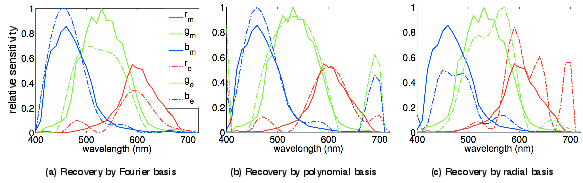
Comparison of recovered camera spectral sensitivies using 3 basis
functions:
(a) Fourier basis, (b) polynomial basis, and (c) radial basis.
The results are worse than that of using the PCA model. The subscripts m
and e stand for the measured and estimated camera spectral sensitivities,
respectively.
|
 |
|
Comparison of four types of basis functions for modeling camera spectral
sensitivity functions:
A -- PCA model, B -- Fourier basis, C -- radial basis and
D -- polynomial basis with the ground truth (E). A color checker is rendered
under D65 with camera spectral sensitiv- ities recovered using these basis
functions, and converted to sRGB. The average color difference between the
renderings (from A to D) and the ground truth (E) are 1.59, 3.54, 2.43 and
7. The gain of the imaging system remains the same for all four basis
functions.
|
 |
|
Simulation of color rendering for cameras:
The images are rendered to
sRGB based on the measured (top row) and estimated (bottom row) camera
spectral sensitivities of Canon 60D. (a) face, (b) beads, and (c) peppers
are from the multispectral image database [25]. The values in the
parentheses are the average color difference (CIEDE00 [11]) between the
bottom and top images in each column. For all three examples, the color
difference is close to one, indicating a close color match.
|
 |
|
Correction of images by Canon5D Mark II:
CC is put in the scene to
locate the white point. The estimated camera spectral sensitivity of
Canon5D Mark II is used to calculate T. Left column: The captured image;
Middle column: the corrected image based on T, and Right column: the corrected
image by dividing the white point (without using T). The images are
rendered in sRGB color space.
|
|
Slides
WACV 2013 Presentation (coming soon)
WACV 2013 Poster (coming soon)
|
Software
Database of camera
spectral sensitivity The database includes the spectral sensitivity functions for 28 cameras,
including professional DSLRs, point-and-shoot, industrial and mobile
cameras. The measurement starts from 400nm to 720nm in an interval of 10nm. The database is in the
form of a text file. Each entry starts with camera name and follows by
measured spectral sensitivities in red, green and blue channel.
Code for recovering camera spectral
sensitivity from a single image This demo MATLAB code shows the recovery of camera spectral
sensitivity with a regular color checker from a single picture under unknown
daylight. An example image captured by a Canon 60D (CR2 RAW format) is
included. The measured camera spectral sensitivity for Canon 60D
and measured daylight are also included for comparison.
|
Spectral Sensitivity Measurement, CVL, University of Tokyo
|
|









